位运算的算法应用

基本介绍

作为算法题的一个大类，位运算相关的题目常常出现在各大公司的面试/笔试题中，下面先说说位运算的基本原理。

位运算使得计算机可以直接对每个比特位进行计算，效率会非常的高。

在 JS 中，位运算会将操作数当作 32 位的二进制串进行计算，如果二进制串超过 32 位，则只保留最后的 32 位进行计算，如：

bash

11100110111110100000000000000110000000000001 # 输入的二进制串
            10100000000000000110000000000001 # 实际使用的二进制串

在 JS 中，位运算有 7 种运算符：

按位与（a & b）：在 a, b 的位表示中，每一个对应的位都为 1 则返回 1，否则返回 0

bash

# 15 & 9 -> 9
  0000 0000 0000 0000 0000 0000 0000 1111
& 0000 0000 0000 0000 0000 0000 0000 1001
  ---------------------------------------
  0000 0000 0000 0000 0000 0000 0000 1001

按位或（a | b）：在 a, b 的位表示中，每一个对应的位，只要有一个为 1 则返回 1，否则返回 0

bash

# 15 | 9 -> 15
  0000 0000 0000 0000 0000 0000 0000 1111
| 0000 0000 0000 0000 0000 0000 0000 1001
  ---------------------------------------
  0000 0000 0000 0000 0000 0000 0000 1111

按位异或（a ^ b）：在 a, b 的位表示中，每一个对应的位，两个不相同则返回 1，相同则返回 0

bash

# 15 ^ 9 -> 6
  0000 0000 0000 0000 0000 0000 0000 1111
| 0000 0000 0000 0000 0000 0000 0000 1001
  ---------------------------------------
  0000 0000 0000 0000 0000 0000 0000 0110

按位非（~a）：反转被操作数的位，即将每一位的 0 转为 1，1 转为 0

bash

# ~15 -> -16
~ 0000 0000 0000 0000 0000 0000 0000 1111
  ---------------------------------------
  1111 1111 1111 1111 1111 1111 1111 0000

左移（a << b）：将 a 的二进制串向左移动 b 位，右边移入 0

bash

# 9 << 2 -> 36
<<  0000 0000 0000 0000 0000 0000 0000 1001
    ---------------------------------------
    0000 0000 0000 0000 0000 0000 0010 0100

有符号右移（a >> b）：把 a 的二进制表示向右移动 b 位，向右被移出的位被丢弃，拷贝最左侧的位以填充左侧。这种右移由于保留最左侧的二进制位，因此可以保留数字原本的正负符号

bash

# 9 >> 2 -> 2
>>  0000 0000 0000 0000 0000 0000 0000 1001
    ---------------------------------------
    0000 0000 0000 0000 0000 0000 0010 0010
# -9 >> 2 -> -3
>>  1111 1111 1111 1111 1111 1111 1111 0111
    ---------------------------------------
    1111 1111 1111 1111 1111 1111 1111 1101

无符号右移（a >>> b）：把 a 的二进制表示向右移动 b 位，向右被移出的位被丢弃，左边空出的位全部填充为 0。这种右移由于左侧直接补 0，因此生成的数字必然是非负数

bash

# 19 >>> 2 -> 4
>>>  0000 0000 0000 0000 0000 0000 0001 0011
     ---------------------------------------
     0000 0000 0000 0000 0000 0000 0010 0010
# -19 >>> 2 -> 1073741819
>>>  1111 1111 1111 1111 1111 1111 1110 1101
     ---------------------------------------
     0011 1111 1111 1111 1111 1111 1111 0011

常用性质

在使用位运算技巧解的算法题中，有以下这些常用的性质：

a 与自身之间的操作

bash

a & a = a
a | a = a
a ^ a = 0

a 与 0 之间的操作

bash

a & 0 = 0
a | 0 = a
a ^ 0 = a

按位与、按位或的还原计算

bash

a | ( a & b ) = a
a & ( a | b ) = a

通过异或完成变量值交换

bash

a ^= b
b ^= a
a ^= b

判断奇偶（通过 & 1 取出最后一个二进制位以达到模 2 的效果）

bash

# 位运算效率更高
a & 1 === a % 2

比较两值是否相等（a ^ a === 0）

bash

a ^ b === 0

将第 i + 1 个二进制位设为 1

bash

a |= 1 << i

将第 i + 1 个二进制位设为 0

bash

a &= ~(1 << i)

取出第 i + 1 个二进制位上的数值

bash

a & (1 << i)

在 a 第 i + 1 个二进制位，插入 b 对应位置的二进制位

bash

a |= 1 << i
a & (b & 1 << i)

删除二进制序列中最后一个值为 1 的位置

bash

a &= (a - 1)

计算 a 的相反数

bash

-a === ~a + 1

保留 a 在二进制位中最后一个 1

bash

a &= (-a)

生成二进制位全为 1 的数

bash

~0

保留 a 二进制序列中最后的 i - 1 位，其余补 0

bash

a & ((1 << i) - 1)

将 a 二进制序列中最后 i - 1 位全部置为 0

bash

a & ~((1 << i) - 1)

判断 a 的二进制序列最高位是否为 1

bash

a < 0 # 最高位为 1 必然是负数

在二进制序列中，仅保留最高位的 1，其他设为 0，输出该数

bash

a = a | (a >> 1)
a = a | (a >> 2)
a = a | (a >> 4)
a = a | (a >> 8)
a = a | (a >> 16)
return (a + 1) >> 1

下面，我们通过一些简单-中等的题目来体验一下位运算解题的巧妙。

题目

78 - 子集

https://leetcode-cn.com/problems/subsets 给你一个整数数组 nums，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。你可以按 任意顺序 返回解集。 示例 1：输入： nums = [1,2,3] 输出： [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

从位运算出发去思考，如果用 0 和 1 标记一个数是否存在于子集中，这样列下来，例子中的输入 [1,2,3] 就会产生下表所示的子集与 0/1 序列的关系，因此我们可以直接遍历这个 0/1 序列，去构建每个子集的数据。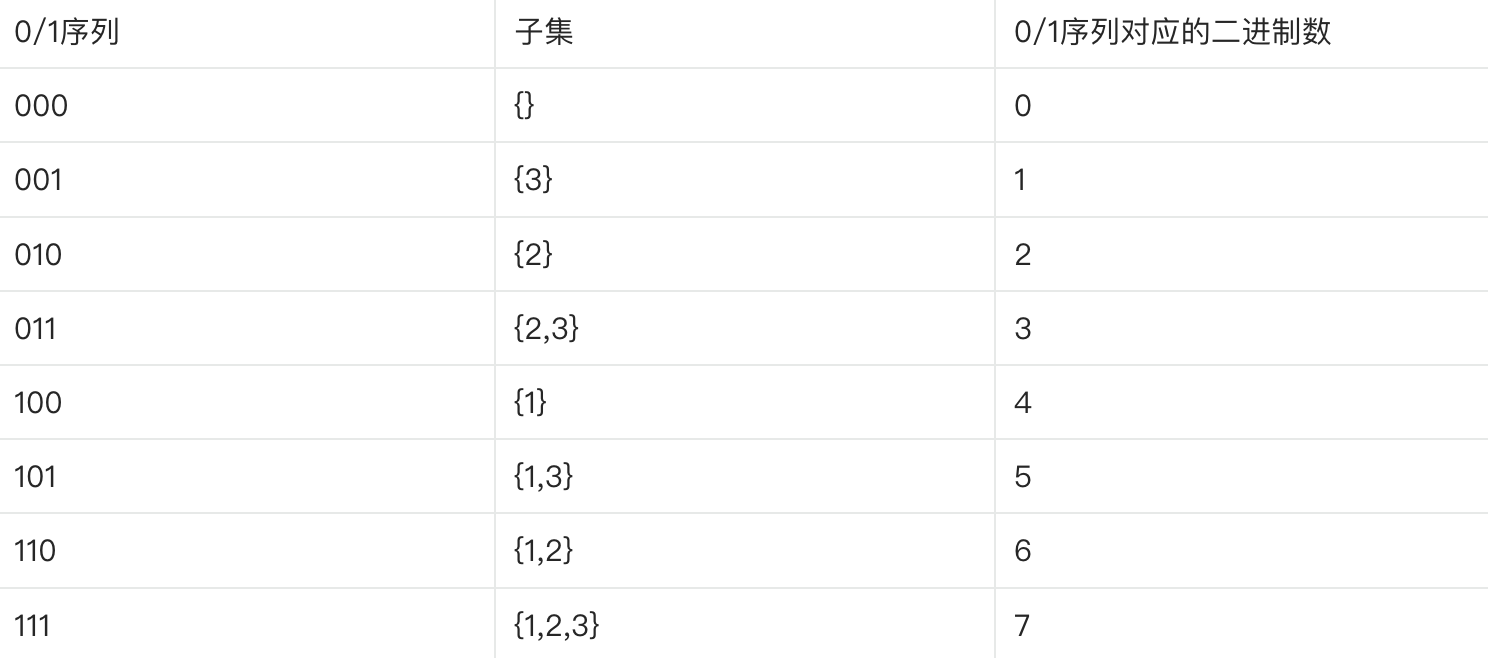

代码的具体实现上，可以通过 1 << nums.length 获取子集的总数；可以利用性质 9 取出相应二进制位上的数值用以构建子集的具体结构。具体的代码实现如下：

javascript

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function(nums) {
  var res = [], len = nums.length
  for (var i = 0; i < (1 << len); i++) {
    var currSubset = []
    for (var j = 0; j <= len; j++) {
      if (i & (1 << j)) currSubset.push(nums[j])
    }
    res.push(currSubset)
  }
  return res
};

复杂度分析：时间复杂度为 O(n2n))，子集的总数为 1 << n 即 2n 种，得 O(2n)，构造每个子集时需要遍历一次原数组，得 O(n)。空间复杂度为 O(n)，只有构造子集时使用的临时数组需要额外空间的开销。

136 - 只出现一次的数字

https://leetcode-cn.com/problems/single-number 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。 说明： 你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？ 示例 1:输入: [2,2,1] 输出: 1 示例 2:输入: [4,1,2,1,2] 输出: 4

从位运算出发去思考，我们可以找到性质 1、2，两个相等的数异或之后为 0，一个数异或 0 等于它本身，那么将数组中所有元素相异或之后，出现 2 次的数字就会全部被约去，剩下只出现 1 次的数字，代码如下：

javascript

/**
 * @param {number[]} nums
 * @return {number}
 */
var singleNumber = function(nums) {
  var res = 0
  for (var i = 0; i < nums.length; i++) {
    res ^= nums[i]
  }
  return res
};

复杂度分析：时间复杂度为 O(n)，因为只有一次遍历数组操作。空间复杂度为 O(1)，没有额外空间开销。

169 - 多数元素

https://leetcode-cn.com/problems/majority-element 给定一个大小为 _n _的数组，找到其中的多数元素。多数元素是指在数组中出现次数 **大于 ** ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的，并且给定的数组总是存在多数元素。 示例 1：输入： [3,2,3] 输出： 3 示例 2：输入： [2,2,1,1,1,2,2] 输出： 2

题干要求的多数元素，出现次数大于 n/2，从位运算出发去思考可以推断，如果将每一个数字都用 32 位二进制序列列出，去统计每一个二进制位是 0 多还是 1 多，则由每一位的多数元素组成的二进制序列，就可以组成最终那个多数元素的数值。代码如下：

javascript

/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function(nums) {
  var res = 0, len = nums.length
  for (var i = 0; i < 32; i++) {
    var ones = 0, zero = 0
    for (var j = 0; j < len; j++) {
      if (ones > len / 2 || zero > len / 2) {
        break
      }
      if ((nums[j] & (1 << i)) === 0) {
        zero++
      } else {
        ones++
      }
    }
    if (ones > zero) res |= 1 << i
  }
  return res
};

复杂度分析：时间复杂度为 O(n)，一次枚举二进制序列上所有的位（32 位），一次遍历整个数组。空间复杂度为 O(1)，没有额外空间开销。

342 - 4 的幂

https://leetcode-cn.com/problems/power-of-four 给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true；否则，返回 false。整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4 ^ x。 示例 1：输入： n = 16 输出： true 示例 2：输入： n = 5 输出： false 示例 3：输入： n = 1 输出： true

将 32 个二进制位铺开来看，一个数为 4 的幂意味着有唯一的数字 1 在序列的奇数位置出现。

bash

0000 0000 0000 0000 0000 0000 0000 0001 # 1
0000 0000 0000 0000 0000 0000 0000 0100 # 4
0000 0000 0000 0000 0000 0000 0001 0000 # 16
0000 0000 0000 0000 0000 0000 0100 0000 # 64

所以可以利用性质 11，根据消去最后一个 1 之后结果是否为 0，可以判断数字的二进制序列中是否存在唯一的 1；另外在循环中使用 >>> 右移操作符直到数字为 0，可以统计出 1 的初始位置。因此代码如下：

javascript

/**
 * @param {number} n
 * @return {boolean}
 */
var isPowerOfFour = function(n) {
  // 是否唯一的 1
  var onlyOne = (n & (n - 1)) === 0
  // 求 1 的位置
  var pos = 0, temp = n
  while (temp !== 0) {
    temp >>>= 1
    pos++
  }
  // 若有唯一的 1，且 1 是奇数，则认为其是 4 的幂
  return onlyOne && ((pos & 1) !== 0)
};

复杂度分析：时间复杂度为 O(1)，解中唯一的循环，是在二进制序列上移动，移动到数字本身为 0，即可求出唯一 1 原来的位置。空间复杂度为 O(1)，没有额外空间开销。

461 - 汉明距离

https://leetcode-cn.com/problems/hamming-distance 两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。给出两个整数 x 和 y，计算它们之间的汉明距离。 注意： 0 ≤ x, y < 231. 示例:输入: x = 1, y = 4 输出: 2 上面的箭头指出了对应二进制位不同的位置。

首先列出示例中两个数的二进制序列：

bash

0000 0000 0000 0000 0000 0000 0000 0001
0000 0000 0000 0000 0000 0000 0000 0100

很明显，只要把两数相异或，二进制位不同的位在结果中即为 1，再使用性质 11 统计结果中 1 的个数，即可得解。因此代码如下：

javascript

/**
 * @param {number} x
 * @param {number} y
 * @return {number}
 */
var hammingDistance = function(x, y) {
  var xorRes = x ^ y, count = 0
  while (xorRes !== 0) {
    xorRes &= (xorRes - 1)
    count++
  }
  return count
};

时间复杂度与空间复杂度均为 O(1)。

1356 - 根据数字二进制下 1 的数目排序

https://leetcode-cn.com/problems/sort-integers-by-the-number-of-1-bits 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 **1 ** 的数目升序排序。如果存在多个数字二进制中 1 的数目相同，则必须将它们按照数值大小升序排列。请你返回排序后的数组。 示例 1：输入： arr = [0,1,2,3,4,5,6,7,8] 输出： [0,1,2,4,8,3,5,6,7] 解释： [0] 是唯一一个有 0 个 1 的数。 [1,2,4,8] 都有 1 个 1。 [3,5,6] 有 2 个 1。 [7] 有 3 个 1 。按照 1 的个数排序得到的结果数组为 [0,1,2,4,8,3,5,6,7]

最暴力的方法，直接调用语言自带的排序函数，对比函数中则使用性质 11 统计 value1 和 value2 二进制序列中 1 的个数，最终 1 的个数不同时按照 1 的个数升序，相同时按照数值大小升序。因此代码如下：

javascript

/**
 * @param {number[]} arr
 * @return {number[]}
 */
var sortByBits = function(arr) {
  return arr.sort((v1, v2) => {
    var temp1 = v1, temp2 = v2, count1 = 0, count2 = 0
    while (temp1 !== 0) {
      temp1 &= temp1 - 1
      count1++
    }
    while (temp2 !== 0) {
      temp2 &= temp2 - 1
      count2++
    }
    return count1 === count2 ? v1 - v2 : count1 - count2
  })
};

复杂度分析：开销全部来自于系统自带的排序函数，JS 的 Array.prototype.sort 是使用快排实现的，因此复杂度与快排一致，时间复杂度为 O(nlogn)，空间复杂度为 O(n)。

总结

在上面列出的题目中，我认为 78 - 子集和 169 - 多数元素是很有代表性的题目，这类问题的共通性在于，题干都可以拆分为多个是非问题的组合。78 - 子集是被拆分为了数组中的每一个数是否存在的问题的集合；而 169 - 多数元素则是被拆分为统计二进制序列中每一个位置上的多数值。因此在解题时可以从这个方向进行思考。

位掩码

虽然本篇是从算法角度切入，但是位运算在日常开发中还有一些实用的小技巧，比如知名 JS 函数库 Lodash 中使用到的位掩码技术。

位掩码通常用于处理多个布尔变量的组合，在 Lodash 中，JS 对象拷贝相关函数的基础函数 baseClone 就使用了位掩码来控制不同的克隆方式。让我们直接来解读一下它的核心代码。

首先，我们需要几个预设的掩码，它们都是由一个仅有唯一 1 的二进制序列组成的（因此它们都是 2 的幂），每个二进制位代表一个开关，而后续的代码中，则可以通过某些二进制运算，来表示各种关系的不同组合：

javascript

const CLONE_DEEP_FLAG = 1    // 0001：深拷贝
const CLONE_FLAT_FLAG = 2    // 0010：拷贝原型链标志位
const CLONE_SYMBOLS_FLAG = 4 // 0100：拷贝 Symbol 类型标志位

然后是 cloneDeep 的代码，它调用了 baseClone，并传入了掩码 CLONE_DEEP_FLAG | CLONE_SYMBOLS_FLAG，这个表达式运算的结果是 5，也就是二进制的 0101。我们发现，通过 | 运算将两个掩码组合，就可以让两个标志位同时变成 1：

javascript

function cloneDeep(value) {
  // cloneDeep 需要深克隆和克隆 Symbol
  // 1 | 4 -> 0001 | 0100 -> 0101
  return baseClone(value, CLONE_DEEP_FLAG | CLONE_SYMBOLS_FLAG)
}

最后找到了 baseClone 的核心代码，这里将刚才传入的 CLONE_DEEP_FLAG | CLONE_SYMBOLS_FLAG 和三个掩码分别进行 & 操作，突然发现这里正是用到了常用性质中的性质 3！这时会发现，我们只要将传入的掩码 bitmask 与各个标志的掩码进行 & 操作，则如果 bitmask 中相应的二进制位为 1，则结果就是该掩码的值；如果 bitmask 中相应的二进制位为 0，则结果就是 0。这样就可以为每个标志位生成其对应的布尔变量，用于后续的函数判断了：

javascript

// 刚才我们传入的值是 1 | 4 = 5
// 因此 isDeep 的值即为 5 & 1 = 1
//   0101
// & 0001
// ------
//   0001
// 可以发现，当传入掩码的二进制序列中存在相应标志位时
// & 操作就会直接返回当前标志位的掩码
// 这样，如果返回的结果为 0，则意味着掩码中不存在相应标志位，结果为 0 == false
// 如果返回的结果大于 0，则意味着掩码中存在相应标志位，结果为任意数字，转换为布尔值为 true
function baseClone(value, bitmask, customizer, key, object, stack) {
  const isDeep = bitmask & CLONE_DEEP_FLAG
  const isFlat = bitmask & CLONE_FLAT_FLAG
  const isFull = bitmask & CLONE_SYMBOLS_FLAG
  ...
}

位运算的算法应用 ​

基本介绍 ​

常用性质 ​

题目 ​

78 - 子集 ​

136 - 只出现一次的数字 ​

169 - 多数元素 ​

342 - 4 的幂 ​

461 - 汉明距离 ​

1356 - 根据数字二进制下 1 的数目排序 ​

总结 ​

位掩码 ​

References ​

位运算的算法应用

基本介绍

常用性质

题目

78 - 子集

136 - 只出现一次的数字

169 - 多数元素

342 - 4 的幂

461 - 汉明距离

1356 - 根据数字二进制下 1 的数目排序

总结

位掩码

References